Для начала рассмотрим круг с радиусом 1 и с центром в (0;0). Для любого αЄR можно провести радиус 0A так, что радианная мера угла между 0A и осью 0x равна α. Направление против часовой стрелки считается положительным. Пусть конец радиуса А имеет координаты (a,b).
Определение синуса
Определение: Число b, равное ординате единичного радиуса, построенного описанным способом, обозначается sinα и называется синусом угла α.
Пример: sin 3π cos3π/2 = 0 0 = 0
Определение косинуса
Определение: Число a, равное абсциссе конца единичного радиуса, построенного описанным способом, обозначается cosα и называется косинусом угла α.
Пример: cos0 cos3π + cos3,5π = 1 (-1) + 0 = 2
Эти примеры используют определение синуса и косинуса угла через координаты конца единичного радиуса и единичной окружности. Для более наглядного представления необходимо нарисовать единичную окружность и отложить на ней соответствующие точки, а затем посчитать их абсциссы для вычисления косинуса и ординаты для вычисления синуса.
Определение тангенса
Определение: Функция tgx=sinx/cosx при x≠π/2+πk, kЄZ, называется котангенсом угла x. Область определения функции tgx это все действительные числа, кроме x=π/2+πn, nЄZ.
Пример: tg0 tgπ = 0 0 = 0
Этот пример аналогичен предыдущему. Для вычисления тангенса угла нужно поделить ординату точки на её абсциссу.
Определение котангенса
Определение: Функция ctgx=cosx/sinx при x≠πk, kЄZ называется котангенсом угла x. Область определения функции ctgx = -все действительные числа кроме точек x=πk, kЄZ.
Рассмотрим пример на обычном прямоугольном треугольнике
Чтобы было понятнее, что же такое косинус, синус, тангенс и котангенс. Рассмотрим пример на обычном прямоугольном треугольнике с углом y и сторонами a,b,c . Гипотенуза с, катеты соответственно a и b. Угол между гипотенузой c и катетом b y.
Определение: Синус угла y - это отношение противолежащего катета к гипотенузе: siny = а/с
Определение: Косинус угла y это отношение прилежащего катета к гипотенузе: сosy= в/с
Определение: Тангенс угла у - это отношение противолежащего катета к прилежащему: tgy = а/в
Определение: Котангенс угла y -это отношение прилежащего катета к противолежащему: ctgy= в/а
Cинус, косинус, тангенс и котангенс называют ещё тригонометрическими функциями. У каждого угла есть свой синус и косинус. И практически у каждого есть свой тангенс и котангенс.
Считается, что если нам дан угол, то его синус, косинус, тангенс и котангенс нам известны! И наоборот. Дан синус, или любая другая тригонометрическая функция соответственно, мы знаем угол. Созданы даже специальные таблицы, где расписаны тригонометрические функции для каждого угла.
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону - гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.

Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.

Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.

Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс - функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.

Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.

Урок по теме «Синус, косинус и тангенс острого угла прямоугольного треугольника»
Цели урока:
образовательные – ввести понятие синус, косинус, тангенс острого угла в прямоугольном треугольнике, исследовать зависимости и соотношения между этими величинами;
развивающие – формирование понятия о синусе, косинусе, тангенсе как функциях от угла, области определения тригонометрических функций, развитие логического мышления, развитие правильной математической речи;
воспитательные – развитие навыка самостоятельной работы, культуры поведения, аккуратности в ведении записей.
Ход урок:
1. Организационный момент
«Образование – это не количество прослушанных уроков, а количество понятых. Так что, если хотите идти вперед, то поспешайте медленно и будьте внимательны»
2. Мотивация урока.
Один мудрец сказал: « Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная. Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но возвысите свою душу».
Мы вместе с вами попробуем провести небольшое исследование. Давайте делиться своими идеями, которые придут вам в голову, и не бойтесь ошибиться, любая мысль может дать нам новое направление поиска. Пусть наши достижения и не покажутся кому-то крупными, но ведь это будут наши собственные достижения!
3. Актуализация опорных знаний.
Какие могут быть углы?
Что такое треугольники?
Основные элементы определяющие треугольник?
Какие бывают треугольники в зависимости от сторон?
Какие бывают треугольники в зависимости от углов?
Что такое катет?
Что такое гипотенуза?
Как называются стороны прямоугольного треугольника?
Какие соотношения между сторонами и углами этого треугольника вы знаете?
Зачем надо знать соотношения между сторонами и углами?
Какие задачи из жизни могут привести к необходимости вычислять неизвестные стороны в треугольнике?
Термин «гипотенуза» происходит от греческого слова «ипонейноуза», обозначающее «тянущаяся над чем-либо», «стягивающая». Слово берет начало от образа древнегреческих арф, на которых струны натягиваются на концах двух взаимно-перпендикулярных подставок. Термин «катет» происходит от греческого слова «катетос», которое означает начало «отвес», «перпендикуляр».
Евклид говорил: «Катеты – это стороны, заключающие прямой угол».
В Древней Греции уже был известен способ построения прямоугольного треугольника на местности. Для этого использовали веревку, на которой были завязаны 13 узелков, на одинаковом расстоянии друг от друга. При строительстве пирамид в Египте именно так изготавливали прямоугольные треугольники. Наверно поэтому прямоугольный треугольник со сторонами 3,4,5 и назвали египетским треугольником.
4. Изучение нового материала.
В древности люди следили за светилами и по этим наблюдениям вели календарь, рассчитывали сроки сева, время разлива рек; корабли на море, караваны на суше ориентировались в пути по звездам. Все это привело к потребности научиться вычислять стороны в треугольнике, две вершины которого находятся на земле, а третья представляется точкой на звездном небе. Исходя из этой потребности и возникла наука – тригонометрия – наука, изучающая связи между сторонами в треугольнике.
Как вы думаете, достаточно ли уже известных нам соотношений для решения таких задач?
Цель сегодняшнего урока – исследовать новые связи и зависимости, вывести соотношения, применяя которые на следующих уроках геометрии, вы сможете такие задачи решать.
Давайте почувствуем себя в роли научных работников и вслед за гениями древности Фалесом, Евклидом, Пифагором пройдем путь поиска истины.
Для этого нам нужна теоретическая база.

Выделите красным цветом угол А и катет ВС.
Выделите зеленым цветом катет АС.
Вычислим, какую часть составляет противолежащий катет для острого угла А к его гипотенузе, для этого составим отношение противолежащего катета к гипотенузе:
Это отношение носит особое название – такое, что каждый человек в каждой точке планеты понимает, что речь идет о числе, представляющем отношение противолежащего катета острого угла к гипотенузе. Это слово синус. Запишите его. Так как слово синус без названия угла теряет всякий смысл, то математическая запись такова:
Теперь составьте отношение прилежащего катета к гипотенузе для острого угла А:
Это отношение имеет название косинус. Его математическая запись:
Рассмотрим еще одно отношение для острого угла А: отношение противолежащего катета к прилежащему катету:
Это отношение носит название тангенс. Его математическая запись:
5. Закрепление нового материала.
Давайте закрепим наши промежуточные открытия.
Синус – это …
Косинус – это …
Тангенс – это..



| sin A = | sin О = | sin A 1 = |
| cos A = | cos О = | cos A 1 = |
| tg A = | tg О = | tg A 1 = |
Решить устно № 88, 889, 892(работа в парах).
Использование полученных знаний для решения практической задачи:
«С башни маяка высотой 70 м виден корабль под углом 3 к горизонту. Каково
расстояние от маяка до корабля?»

Задача решается фронтально. В ходе обсуждения делаем чертеж и необходимые записи на доске и в тетрадях.
При решении задачи используются таблицы Брадиса.
Рассмотреть решение задачи с.175.
Решить №902(1).
6. Физминутка для глаз.
Не поворачивая головы, обведите взглядом стену класса по периметру по часовой стрелке, классную доску по периметру против часовой стрелки, треугольник, изображенный на стенде по часовой стрелке и равный ему треугольник против часовой стрелки. Поверните голову налево и посмотрите на линию горизонта, а теперь на кончик своего носа. Закройте глаза, сосчитайте до 5, откройте глаза и …
Мы ладонь к глазам приставим,
Ноги крепкие расставим.
Поворачиваясь вправо,
Оглядимся величаво.
И налево надо тоже
Поглядеть из под ладошек.
И – направо! И еще
Через левое плечо!
а теперь продолжим работу.
7. Самостоятельная работа учащихся.
Решить № .
8.Итоги урока. Рефлексия. Д/з.
Что вы узнали нового? На уроке:
вы рассматривали …
вы анализировали …
вы получили …
вы сделали вывод …
вы пополнили словарный запас следующими терминами …
Мировая наука начиналась с геометрии. Человек не может по настоящему развиваться культурно и духовно, если он не изучал в школе геометрию. Геометрия возникла не только из практических, но и духовных потребностей человека.
Вот как поэтично объяснилась в любви к геометрии
Геометрию люблю…
Геометрию учу, потому что я люблю
Геометрия нужна, без нее нам никуда.
Синус, косинус, окружность – все здесь важно,
Все здесь нужно,
Только надо очень четко все учить и познавать,
Делать вовремя заданья и контрольные решать.
Учителя считают, что каждый школьник должен уметь проводить расчёты, знать тригонометрические формулы, но далеко не каждый преподаватель объясняет, что такое синус и косинус. Каков их смысл, где они используются? Почему мы говорим про треугольники, а в учебнике нарисована окружность? Попробуем связать все факты воедино.
Школьный предмет
Изучение тригонометрии начинается обычно в 7-8 классе средней школы. В это время учащимся объясняют, что такое синус и косинус, предлагают решать геометрические задачи с применением этих функций. Позже появляются более сложные формулы и выражения, которые требуется алгебраическим способом преобразовывать (формулы двойного и половинного угла, степенные функции), проводится работа с тригонометрической окружностью.
Однако учителя далеко не всегда могут доходчиво объяснить смысл используемых понятий и применимость формул. Поэтому ученик зачастую не видит смысла в данном предмете, а заученная информация быстро забывается. Однако стоит один раз объяснить старшекласснику, например, связь между функцией и колебательным движением, и логическая связь запомнится на многие годы, а шутки на тему бесполезности предмета уйдут в прошлое.
Использование
Заглянем ради любопытства в различные разделы физики. Хотите определить дальность полёта снаряда? Или высчитываете силу трения между объектом и некой поверхностью? Раскачиваете маятник, следите за лучами, проходящими сквозь стекло, высчитываете индукцию? Практически в любой формуле фигурируют тригонометрические понятия. Так что такое синус и косинус?
Определения
Синус угла представляет собой отношение противолежащего катета к гипотенузе, косинус - прилежащего катета всё к той же гипотенузе. Здесь нет совершенно ничего сложного. Возможно, учеников обычно смущают значения, которые они видят в тригонометрической таблице, ведь там фигурируют квадратные корни. Да, получать из них десятичные дроби не очень удобно, но кто сказал, что все числа в математике должны быть ровными?

На самом деле в задачниках по тригонометрии можно найти забавную подсказку: большинство ответов здесь ровные и в худшем случае содержат корень из двух или из трёх. Вывод прост: если у вас в ответе получилась «многоэтажная» дробь, перепроверьте решение на предмет ошибок в расчётах или в рассуждениях. И вы их, скорее всего, найдете.
Что нужно запомнить
Как и в любой науке, в тригонометрии есть такие данные, которые необходимо выучить.
Во-первых, следует запомнить числовые значения для синусов, косинусов прямоугольного треугольника 0 и 90, а также 30, 45 и 60 градусов. Эти показатели встречаются в девяти из десяти школьных задач. Подглядывая эти значения в учебнике, вы потеряете много времени, а на контрольной или экзамене посмотреть и вовсе будет негде.

Нужно помнить, что значение обеих функций не может превышать единицу. Если где-либо в расчетах вы получите значение, выходящее за пределы диапазона 0-1, остановитесь и решите задачу заново.
Сумма квадратов синуса и косинуса равна единице. Если вы уже нашли одно из значений, воспользуйтесь этой формулой для нахождения оставшегося.
Теоремы
В базовой тригонометрии существует две основные теоремы: синусов и косинусов.
Первая гласит, что отношение каждой стороны треугольника к синусу противолежащего угла одинаково. Вторая - что квадрат любой стороны можно получить, если сложить квадраты двух оставшихся сторон и вычесть удвоенное их произведение, умноженное на косинус лежащего между ними угла.
Таким образом, если в теорему косинусов подставить значение угла в 90 градусов, мы получим… теорему Пифагора. Теперь, если требуется высчитать площадь фигуры, не являющейся прямоугольным треугольником, можно больше не переживать - две рассмотренные теоремы существенно упростят решение задачи.
Цели и задачи
Изучение тригонометрии значительно упростится, когда вы осознаете один простой факт: все выполняемые вами действия направлены на достижения всего одной цели. Любые параметры треугольника могут быть найдены, если вы знаете о нём самый минимум информации - это может быть величина одного угла и длины двух сторон или, например, три стороны.
Для определения синуса, косинуса, тангенса любого угла этих данных достаточно, с их же помощью можно легко высчитать площадь фигуры. Практически всегда в качестве ответа требуется привести одно из упомянутых значений, а найти их можно по одним и тем же формулам.
Нестыковки при изучении тригонометрии
Одним из непонятных вопросов, которых школьники предпочитают избегать, является обнаружение связи между различными понятиями в тригонометрии. Казалось бы, для изучения синусов и косинусов углов используются треугольники, но обозначения почему-то часто встречаются на рисунке с окружностью. Кроме того, существует и вовсе непонятный волнообразный график под названием синусоида, не имеющий никакого внешнего сходства ни с окружностью, ни с треугольниками.

Более того, углы измеряются то в градусах, то в радианах, а число Пи, записывающееся просто как 3,14 (без единиц измерения), почему-то фигурирует в формулах, соответствуя 180 градусам. Как всё это связано между собой?
Единицы измерения
Почему число Пи равняется именно 3,14? Помните ли вы, что это за значение? Это количество радиусов, умещающихся в дуге на половине окружности. Если диаметр круга - 2 сантиметра, длина окружности составит 3,14*2, или 6,28.
Второй момент: возможно, вы замечали сходство слов «радиан» и «радиус». Дело в том, что один радиан численно равен величине угла, отложенного из центра окружности на дугу длиной в один радиус.
Теперь совместим полученные знания и поймем, почему сверху на оси координат в тригонометрии пишется «Пи пополам», а слева - «Пи». Это угловая величина, измеренная в радианах, ведь полукруг - это 180 градусов, или 3,14 радиана. А там, где есть градусы, есть синусы и косинусы. Треугольник же легко провести от нужной точки, отложив отрезки к центру и на ось координат.
Заглянем в будущее
Тригонометрия, изучаемая в школе, имеет дело с прямолинейной системой координат, где, как бы это странно ни звучало, прямая - это прямая.
Но есть и более сложные способы работы с пространством: сумма углов треугольника здесь будет больше 180 градусов, а прямая в нашем представлении будет выглядеть как самая настоящая дуга.

Перейдем от слов к делу! Возьмите яблоко. Сделайте ножом три надреза, чтобы при взгляде сверху получался треугольник. Выньте получившийся кусок яблока и посмотрите на «рёбра», где заканчивается кожура. Они вовсе не прямые. Фрукт в ваших руках условно можно назвать круглым, а теперь представьте, какими сложными должны быть формулы, с помощью которых можно найти площадь вырезанного куска. А ведь некоторые специалисты решают такие задачи ежедневно.
Тригонометрические функции в жизни
Обращали ли вы внимание, что самый короткий маршрут самолёта из точки А в точку Б на поверхности нашей планеты имеет ярко выраженную форму дуги? Причина проста: Земля имеет форму шара, а значит, с помощью треугольников многого не вычислишь - здесь приходится использовать более сложные формулы.

Не обойтись без синуса/косинуса острого угла в любых вопросах, связанных с космосом. Интересно, что здесь сходится целое множество факторов: тригонометрические функции требуются при расчётах движения планет по окружностям, эллипсам и различным траекториям более сложных форм; процесса запуска ракет, спутников, шаттлов, отстыковки исследовательских аппаратов; наблюдении за далёкими звёздами и изучении галактик, до которых человек в обозримом будущем добраться не сможет.
В целом поле для деятельности человека, владеющего тригонометрией, очень широко и, по-видимому, со временем будет только расширяться.
Заключение
Сегодня мы узнали или, во всяком случае, повторили, что такое синус и косинус. Это понятия, которых не нужно бояться - стоит захотеть, и вы поймете их смысл. Помните, что тригонометрия - это не цель, а лишь инструмент, который можно использовать для удовлетворения реальных человеческих потребностей: строить дома, обеспечивать безопасность движения, даже осваивать просторы вселенной.

Действительно, сама по себе наука может казаться скучной, но как только вы найдете в ней способ достижения собственных целей, самореализации, процесс обучения станет интересным, а ваша личная мотивация возрастёт.
В качестве домашнего задания попробуйте найти способы применить тригонометрические функции в той сфере деятельности, которая интересна лично вам. Пофантазируйте, включите воображение, и тогда наверняка окажется, что новые знания пригодятся вам в будущем. Да и кроме того, математика полезна для общего развития мышления.
Понятия синуса, косинуса, тангенса и котангенса являются основными категориями тригонометрии — раздела математики, и неразрывно связаны с определением угла. Владение этой математической наукой требует запоминания и понимания формул и теорем, а также развитого пространственного мышления. Именно поэтому у школьников и студентов тригонометрические вычисления нередко вызывают трудности. Чтобы побороть их, следует подробнее познакомиться с тригонометрическими функциями и формулами.
Понятия в тригонометрии
Чтобы разобраться в базовых понятиях тригонометрии, следует сначала определиться с тем, что такое прямоугольный треугольник и угол в окружности, и почему именно с ними связаны все основные тригонометрические вычисления. Треугольник, в котором один из углов имеет величину 90 градусов, является прямоугольным. Исторически эта фигура часто использовалась людьми в архитектуре, навигации, искусстве, астрономии. Соответственно, изучая и анализируя свойства этой фигуры, люди пришли к вычислению соответствующих соотношений её параметров.
Основные категории, связанные с прямоугольными треугольниками — гипотенуза и катеты. Гипотенуза — сторона треугольника, лежащая против прямого угла. Катеты, соответственно, это остальные две стороны. Сумма углов любых треугольников всегда равна 180 градусам.
Сферическая тригонометрия — раздел тригонометрии, который не изучается в школе, однако в прикладных науках типа астрономии и геодезии, учёные пользуются именно им. Особенность треугольника в сферической тригонометрии в том, что он всегда имеет сумму углов более 180 градусов.
Углы треугольника
 В прямоугольном треугольнике синусом угла является отношение катета, противолежащего искомому углу, к гипотенузе треугольника. Соответственно, косинус — это отношение прилежащего катета и гипотенузы. Оба эти значения всегда имеют величину меньше единицы, так как гипотенуза всегда длиннее катета.
В прямоугольном треугольнике синусом угла является отношение катета, противолежащего искомому углу, к гипотенузе треугольника. Соответственно, косинус — это отношение прилежащего катета и гипотенузы. Оба эти значения всегда имеют величину меньше единицы, так как гипотенуза всегда длиннее катета.
Тангенс угла — величина, равная отношению противолежащего катета к прилежащему катету искомого угла, или же синуса к косинусу. Котангенс, в свою очередь, это отношение прилежащего катета искомого угла к противолежащему кактету. Котангенс угла можно также получить, разделив единицу на значение тангенса.
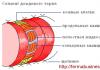
Единичная окружность
Единичная окружность в геометрии — окружность, радиус которой равен единице. Такая окружность строится в декартовой системе координат, при этом центр окружности совпадает с точкой начала координат, а начальное положение вектора радиуса определено по положительному направлению оси Х (оси абсцисс). Каждая точка окружности имеет две координаты: ХХ и YY, то есть координаты абсцисс и ординат. Выбрав на окружности любую точку в плоскости ХХ, и опустив с неё перпендикуляр на ось абсцисс, получаем прямоугольный треугольник, образованный радиусом до выбранной точки (обозначим её буквой С), перпендикуляром, проведённым до оси Х (точка пересечения обозначается буквой G), а отрезком оси абсцисс между началом координат (точка обозначена буквой А) и точкой пересечения G. Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG. Аналогично, sin α=CG.
Кроме того, зная эти данные, можно определить координату точки С на окружности, так как cos α=AG, а sin α=CG, значит, точка С имеет заданные координаты (cos α;sin α). Зная, что тангенс равен отношению синуса к косинусу, можно определить, что tg α = y/х, а ctg α = х/y. Рассматривая углы в отрицательной системе координат, можно рассчитать, что значения синуса и косинуса некоторых углов могут быть отрицательными.
Вычисления и основные формулы
Значения тригонометрических функций
Рассмотрев сущность тригонометрических функций через единичную окружность, можно вывести значения этих функций для некоторых углов. Значения перечислены в таблице ниже.
Простейшие тригонометрические тождества
Уравнения, в которых под знаком тригонометрической функции присутствует неизвестное значение, называются тригонометрическими. Тождества со значением sin х = α, k — любое целое число:
- sin х = 0, х = πk.
- 2. sin х = 1, х = π/2 + 2πk.
- sin х = -1, х = -π/2 + 2πk.
- sin х = а, |a| > 1, нет решений.
- sin х = а, |a| ≦ 1, х = (-1)^k * arcsin α + πk.
Тождества со значением cos х = а, где k — любое целое число:
- cos х = 0, х = π/2 + πk.
- cos х = 1, х = 2πk.
- cos х = -1, х = π + 2πk.
- cos х = а, |a| > 1, нет решений.
- cos х = а, |a| ≦ 1, х = ±arccos α + 2πk.
Тождества со значением tg х = а, где k — любое целое число:
- tg х = 0, х = π/2 + πk.
- tg х = а, х = arctg α + πk.
Тождества со значением ctg х = а, где k — любое целое число:
- ctg х = 0, х = π/2 + πk.
- ctg х = а, х = arcctg α + πk.
Формулы приведения
Эта категория постоянных формул обозначает методы, с помощью которых можно перейти от тригонометрических функций вида к функциям аргумента, то есть привести синус, косинус, тангенс и котангенс угла любого значения к соответствующим показателям угла интервала от 0 до 90 градусов для большего удобства вычислений.
Формулы приведения функций для синуса угла выглядят таким образом:
- sin(900 — α) = α;
- sin(900 + α) = cos α;
- sin(1800 — α) = sin α;
- sin(1800 + α) = -sin α;
- sin(2700 — α) = -cos α;
- sin(2700 + α) = -cos α;
- sin(3600 — α) = -sin α;
- sin(3600 + α) = sin α.
Для косинуса угла:
- cos(900 — α) = sin α;
- cos(900 + α) = -sin α;
- cos(1800 — α) = -cos α;
- cos(1800 + α) = -cos α;
- cos(2700 — α) = -sin α;
- cos(2700 + α) = sin α;
- cos(3600 — α) = cos α;
- cos(3600 + α) = cos α.
Использование вышеуказанных формул возможно при соблюдении двух правил. Во-первых, если угол можно представить как значение (π/2 ± a) или (3π/2 ± a), значение функции меняется:
- с sin на cos;
- с cos на sin;
- с tg на ctg;
- с ctg на tg.
Значение функции остаётся неизменным, если угол может быть представлен как (π ± a) или (2π ± a).
Во-вторых, знак приведенной функции не изменяется: если он изначально был положительным, таким и остаётся. Аналогично с отрицательными функциями.
Формулы сложения
Эти формулы выражают величины синуса, косинуса, тангенса и котангенса суммы и разности двух углов поворота через их тригонометрические функции. Обычно углы обозначаются как α и β.
Формулы имеют такой вид:
- sin(α ± β) = sin α * cos β ± cos α * sin.
- cos(α ± β) = cos α * cos β ∓ sin α * sin.
- tg(α ± β) = (tg α ± tg β) / (1 ∓ tg α * tg β).
- ctg(α ± β) = (-1 ± ctg α * ctg β) / (ctg α ± ctg β).
Эти формулы справедливы для любых величин углов α и β.
Формулы двойного и тройного угла
Тригонометрические формулы двойного и тройного угла — это формулы, которые связывают функции углов 2α и 3α соответственно, с тригонометрическими функциями угла α. Выводятся из формул сложения:
- sin2α = 2sinα*cosα.
- cos2α = 1 — 2sin^2 α.
- tg2α = 2tgα / (1 — tg^2 α).
- sin3α = 3sinα — 4sin^3 α.
- cos3α = 4cos^3 α — 3cosα.
- tg3α = (3tgα — tg^3 α) / (1-tg^2 α).
Переход от суммы к произведению
Учитывая, что 2sinx*cosy = sin(x+y) + sin(x-y), упростив эту формулу, получаем тождество sinα + sinβ = 2sin(α + β)/2 * cos(α − β)/2. Аналогично sinα — sinβ = 2sin(α — β)/2 * cos(α + β)/2; cosα + cosβ = 2cos(α + β)/2 * cos(α − β)/2; cosα — cosβ = 2sin(α + β)/2 * sin(α − β)/2; tgα + tgβ = sin(α + β) / cosα * cosβ; tgα — tgβ = sin(α — β) / cosα * cosβ; cosα + sinα = √2sin(π/4 ∓ α) = √2cos(π/4 ± α).
Переход от произведения к сумме
Эти формулы следуют из тождеств перехода суммы в произведение:
- sinα * sinβ = 1/2*;
- cosα * cosβ = 1/2*;
- sinα * cosβ = 1/2*.
Формулы понижения степени
В этих тождествах квадратную и кубическую степени синуса и косинуса можно выразить через синус и косинус первой степени кратного угла:
- sin^2 α = (1 — cos2α)/2;
- cos^2 α = (1 + cos2α)/2;
- sin^3 α = (3 * sinα — sin3α)/4;
- cos^3 α = (3 * cosα + cos3α)/4;
- sin^4 α = (3 — 4cos2α + cos4α)/8;
- cos^4 α = (3 + 4cos2α + cos4α)/8.
Универсальная подстановка
Формулы универсальной тригонометрической подстановки выражают тригонометрические функции через тангенс половинного угла.
- sin x = (2tgx/2) * (1 + tg^2 x/2), при этом х = π + 2πn;
- cos x = (1 — tg^2 x/2) / (1 + tg^2 x/2), где х = π + 2πn;
- tg x = (2tgx/2) / (1 — tg^2 x/2), где х = π + 2πn;
- ctg x = (1 — tg^2 x/2) / (2tgx/2), при этом х = π + 2πn.
Частные случаи
Частные случаи простейших тригонометрических уравнений приведены ниже (k — любое целое число).
Частные для синуса:
| Значение sin x | Значение x |
|---|---|
| 0 | πk |
| 1 | π/2 + 2πk |
| -1 | -π/2 + 2πk |
| 1/2 | π/6 + 2πk или 5π/6 + 2πk |
| -1/2 | -π/6 + 2πk или -5π/6 + 2πk |
| √2/2 | π/4 + 2πk или 3π/4 + 2πk |
| -√2/2 | -π/4 + 2πk или -3π/4 + 2πk |
| √3/2 | π/3 + 2πk или 2π/3 + 2πk |
| -√3/2 | -π/3 + 2πk или -2π/3 + 2πk |
Частные для косинуса:
| Значение cos x | Значение х |
|---|---|
| 0 | π/2 + 2πk |
| 1 | 2πk |
| -1 | 2 + 2πk |
| 1/2 | ±π/3 + 2πk |
| -1/2 | ±2π/3 + 2πk |
| √2/2 | ±π/4 + 2πk |
| -√2/2 | ±3π/4 + 2πk |
| √3/2 | ±π/6 + 2πk |
| -√3/2 | ±5π/6 + 2πk |
Частные для тангенса:
| Значение tg x | Значение х |
|---|---|
| 0 | πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3/3 | π/6 + πk |
| -√3/3 | -π/6 + πk |
| √3 | π/3 + πk |
| -√3 | -π/3 + πk |
Частные для котангенса:
| Значение ctg x | Значение x |
|---|---|
| 0 | π/2 + πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3 | π/6 + πk |
| -√3 | -π/3 + πk |
| √3/3 | π/3 + πk |
| -√3/3 | -π/3 + πk |
Теоремы
Теорема синусов
Существует два варианта теоремы — простой и расширенный. Простая теорема синусов: a/sin α = b/sin β = c/sin γ. При этом, a, b, c — стороны треугольника, и α, β, γ — соответственно, противолежащие углы.
Расширенная теорема синусов для произвольного треугольника: a/sin α = b/sin β = c/sin γ = 2R. В этом тождестве R обозначает радиус круга, в который вписан заданный треугольник.
Теорема косинусов
Тождество отображается таким образом: a^2 = b^2 + c^2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
Теорема тангенсов
Формула выражает связь между тангенсами двух углов, и длиной сторон, им противолежащих. Стороны обозначены как a, b, c, а соответствующие противолежащие углы — α, β, γ. Формула теоремы тангенсов: (a — b) / (a+b) = tg((α — β)/2) / tg((α + β)/2).
Теорема котангенсов
Связывает радиус вписанной в треугольник окружности с длиной его сторон. Если a, b, c — стороны треугольника, и А, В, С, соответственно, противолежащие им углы, r — радиус вписанной окружности, и p — полупериметр треугольника, справедливы такие тождества:
- ctg A/2 = (p-a)/r;
- ctg B/2 = (p-b)/r;
- ctg C/2 = (p-c)/r.
Прикладное применение

Тригонометрия — не только теоретическая наука, связанная с математическими формулами. Её свойствами, теоремами и правилами пользуются на практике разные отрасли человеческой деятельности — астрономия, воздушная и морская навигация, теория музыки, геодезия, химия, акустика, оптика, электроника, архитектура, экономика, машиностроение, измерительные работы, компьютерная графика, картография, океанография, и многие другие.
Синус, косинус, тангенс и котангенс — основные понятия тригонометрии, с помощью которых математически можно выразить соотношения между углами и длинами сторон в треугольнике, и найти искомые величины через тождества, теоремы и правила.